Difference between revisions of "January 23, 2019"
| Line 6: | Line 6: | ||
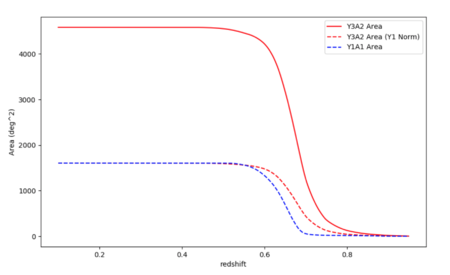
[[File:Volumelimited_rm.png|thumb|left|upright=1.5|alt=Alt text|Plot of sky coverage versus redshift for the RedMaPPer volume-limited cluster catalog. The red line represents Y3 data (and is from a couple iterations ago, but I image that it's not too different from the current iteration.) The blue line represents previous Y1 data and the dashed red line is Y3 data with the norm scaled to Y1, so that you can see that Y3 goes slightly farther out.]] | [[File:Volumelimited_rm.png|thumb|left|upright=1.5|alt=Alt text|Plot of sky coverage versus redshift for the RedMaPPer volume-limited cluster catalog. The red line represents Y3 data (and is from a couple iterations ago, but I image that it's not too different from the current iteration.) The blue line represents previous Y1 data and the dashed red line is Y3 data with the norm scaled to Y1, so that you can see that Y3 goes slightly farther out.]] | ||
| − | I am currently using the Volume Limited catalog with lambda > 5. The full catalog contains ~300,000 clusters. The part of the catalog overlapping with the ACT y-map region contains ~80,000 clusters. | + | I am currently using the Volume Limited catalog with lambda > 5. The full catalog contains ~300,000 clusters from z=0.1 to z=0.9. The part of the catalog overlapping with the ACT y-map region contains ~80,000 clusters. |
== Motivation for Finding the Correlation Scale == | == Motivation for Finding the Correlation Scale == | ||
| Line 12: | Line 12: | ||
When I plotted all the cluster positions and smoothed them to a four arcminute beam, they were so separated that this did not create the nearly smooth number-density map that we want. Furthermore, if I cut the catalog down into small redshift slices, the clusters are even more sparse. Therefore, I want to know what the optimal scale is to be smoothing on, to create a useful orientation map which will contain relevant information about super-clustering. One way to figure out the best scale is to find the cluster correlation scale: at what distance are clusters most clustered? Another question I have is: what is the ideal distance to slice the cluster sample at? A comoving distance of 30 Mpc? 100? Larger? Examining the cluster correlation function for various slices in redshift will tell us the information on super-clustering scales that we need. | When I plotted all the cluster positions and smoothed them to a four arcminute beam, they were so separated that this did not create the nearly smooth number-density map that we want. Furthermore, if I cut the catalog down into small redshift slices, the clusters are even more sparse. Therefore, I want to know what the optimal scale is to be smoothing on, to create a useful orientation map which will contain relevant information about super-clustering. One way to figure out the best scale is to find the cluster correlation scale: at what distance are clusters most clustered? Another question I have is: what is the ideal distance to slice the cluster sample at? A comoving distance of 30 Mpc? 100? Larger? Examining the cluster correlation function for various slices in redshift will tell us the information on super-clustering scales that we need. | ||
| − | == Method == | + | == Method and Plots == |
1) Create a map of Redmapper clusters as point sources. I am smoothing the point sources to 2'. I start by using a redshift slice that corresponds to the first comoving 100 Mpc of the sample. This has 2,810 clusters from 0.1 < z < 0.124. | 1) Create a map of Redmapper clusters as point sources. I am smoothing the point sources to 2'. I start by using a redshift slice that corresponds to the first comoving 100 Mpc of the sample. This has 2,810 clusters from 0.1 < z < 0.124. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | 2) Stack each cluster on top of each other with its surrounding field oriented randomly. Figure 2 shows the stack. | ||
| − | + | 3) I move out from the centre of this image in radius bins of 1'. Within each radius bin, I sum up the flux in that annulus and divide by the area of the annulus. This gives the flux per unit area at each radius step, which should be representative of the scales at which clusters typically lie from each other. Figure 3 shows this plot. The peak occurs at 8', so the cluster correlation scale for this redshift slice is 8'. | |
| − | [[File:Clust corr z.1toz.124 2am.png|thumb|left|upright=1.5|alt=Alt text|Starting 1' from the center, I sum all the pixel values in the above image in an annulus with the inner circle and outer circle separated by 1'. The plot starts off high because of the flux from the center, goes to 0 when the annuli enter the 'no-man's land', and peaks at 8' where clusters are typically separated. ]] | + | |
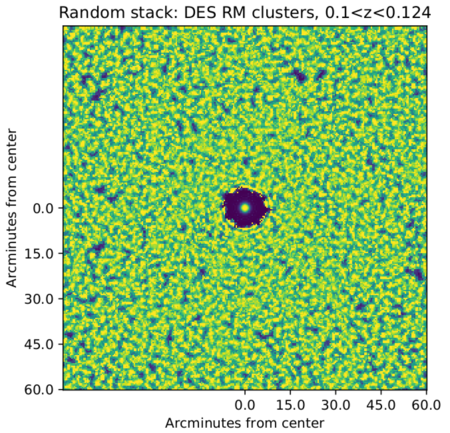
| + | [[File:Random stack rm 2am.png|thumb|left|upright=1.5|alt=Alt text|Figure 2: Stack of clusters, as points smoothed to 2' FWHM, with random orientation. The stacked clusters in the center are clearly separated from the typical nearest neighbor distance.]] | ||
| + | |||
| + | [[File:Clust corr z.1toz.124 2am.png|thumb|left|upright=1.5|alt=Alt text|Figure 3: Starting 1' from the center, I sum all the pixel values in the above image in an annulus with the inner circle and outer circle separated by 1'. The plot starts off high because of the flux from the center, goes to 0 when the annuli enter the 'no-man's land', and peaks at 8' where clusters are typically separated. ]] | ||
| + | |||
| + | Figure 4 shows the map of DES cluster overlapping with the ACT sky coverage region, smoothed to 8'. | ||
| + | |||
| + | == Next Steps == | ||
| + | I may try other smoothing scales to make sure that does not affect the result. I will repeat the process for slices of 100 Mpc comoving distance at higher and higher redshifts, to observe how the scale changes with redshift. The further away I go, the correlation scale in arcminutes should get smaller. I could also convert this scale to comoving distance at the different redshifts to see how the comoving scale changes. | ||
Revision as of 17:33, 23 January 2019
Cluster Correlation Scale
Overview of RedMaPPer Y3 Data
The RedMaPPer Y3 data is divided into two types of catalog: volume-limited and full. The volume-limited catalog is limited in redshift as shown in Figure 1. The full catalog does not apply the same redshift limit. For either type, you can then choose between a catalog which include clusters of richness greater than 5, or richness greater than 20.
I am currently using the Volume Limited catalog with lambda > 5. The full catalog contains ~300,000 clusters from z=0.1 to z=0.9. The part of the catalog overlapping with the ACT y-map region contains ~80,000 clusters.
Motivation for Finding the Correlation Scale
When I plotted all the cluster positions and smoothed them to a four arcminute beam, they were so separated that this did not create the nearly smooth number-density map that we want. Furthermore, if I cut the catalog down into small redshift slices, the clusters are even more sparse. Therefore, I want to know what the optimal scale is to be smoothing on, to create a useful orientation map which will contain relevant information about super-clustering. One way to figure out the best scale is to find the cluster correlation scale: at what distance are clusters most clustered? Another question I have is: what is the ideal distance to slice the cluster sample at? A comoving distance of 30 Mpc? 100? Larger? Examining the cluster correlation function for various slices in redshift will tell us the information on super-clustering scales that we need.
Method and Plots
1) Create a map of Redmapper clusters as point sources. I am smoothing the point sources to 2'. I start by using a redshift slice that corresponds to the first comoving 100 Mpc of the sample. This has 2,810 clusters from 0.1 < z < 0.124.
2) Stack each cluster on top of each other with its surrounding field oriented randomly. Figure 2 shows the stack.
3) I move out from the centre of this image in radius bins of 1'. Within each radius bin, I sum up the flux in that annulus and divide by the area of the annulus. This gives the flux per unit area at each radius step, which should be representative of the scales at which clusters typically lie from each other. Figure 3 shows this plot. The peak occurs at 8', so the cluster correlation scale for this redshift slice is 8'.

Figure 4 shows the map of DES cluster overlapping with the ACT sky coverage region, smoothed to 8'.
Next Steps
I may try other smoothing scales to make sure that does not affect the result. I will repeat the process for slices of 100 Mpc comoving distance at higher and higher redshifts, to observe how the scale changes with redshift. The further away I go, the correlation scale in arcminutes should get smaller. I could also convert this scale to comoving distance at the different redshifts to see how the comoving scale changes.