Feb 5, 2019 - Dig into where Jason's skewness is coming from
Jason sees high skewness / kurtosis with his difference maps; I do not with my top hat filters (smoothed or not around the edges). What do I throw out and Jason keeps?
Focusing on one of the Jason's difference maps with large skewness, difference between maps smoothed with [math]\displaystyle{ \theta_\mathrm{fwhm} = \frac{2\pi*N_\mathrm{bands}}{3*i*N_\mathrm{side}} }[/math] with [math]\displaystyle{ i = 15, 16 }[/math]. Jason uses [math]\displaystyle{ N_\mathrm{bands} = 32 }[/math] and [math]\displaystyle{ N_\mathrm{side} = 4096 }[/math].
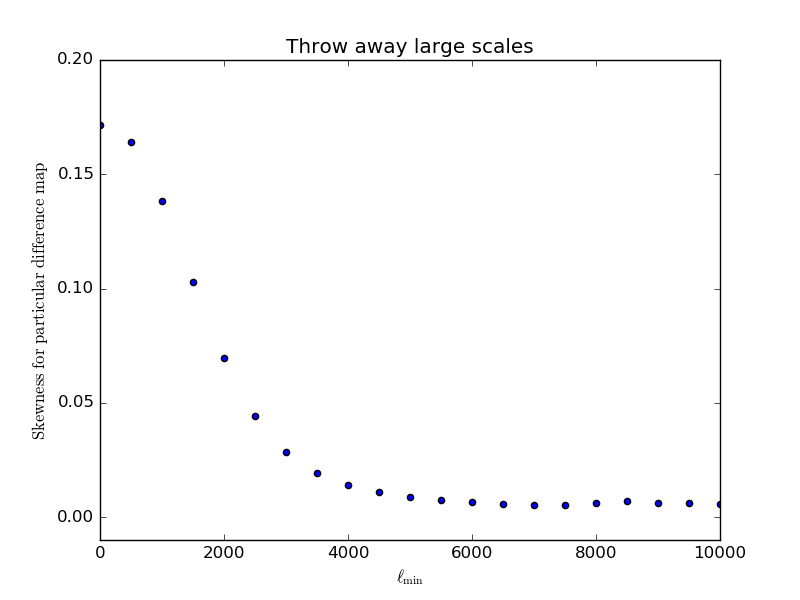
We check what happens if we erase some of the largest or smallest scales in the map, up to given [math]\displaystyle{ \ell_\mathrm{min} }[/math] / down from a given [math]\displaystyle{ \ell_\mathrm{max} }[/math]:
Curiously enough, the support for large skewness seems to be at [math]\displaystyle{ \ell \lt 5000 }[/math], which clashes with the intuition we got from the [math]\displaystyle{ \Delta \ell = 500 }[/math] top hat filters.
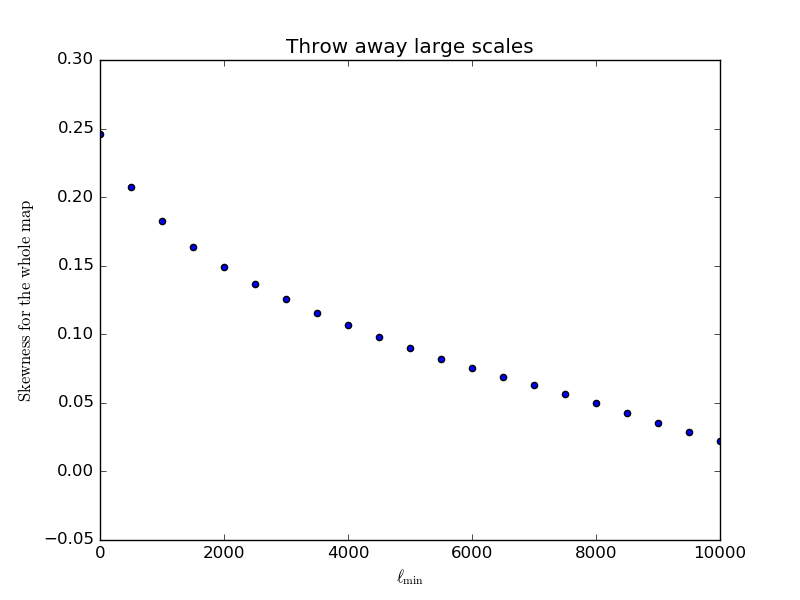
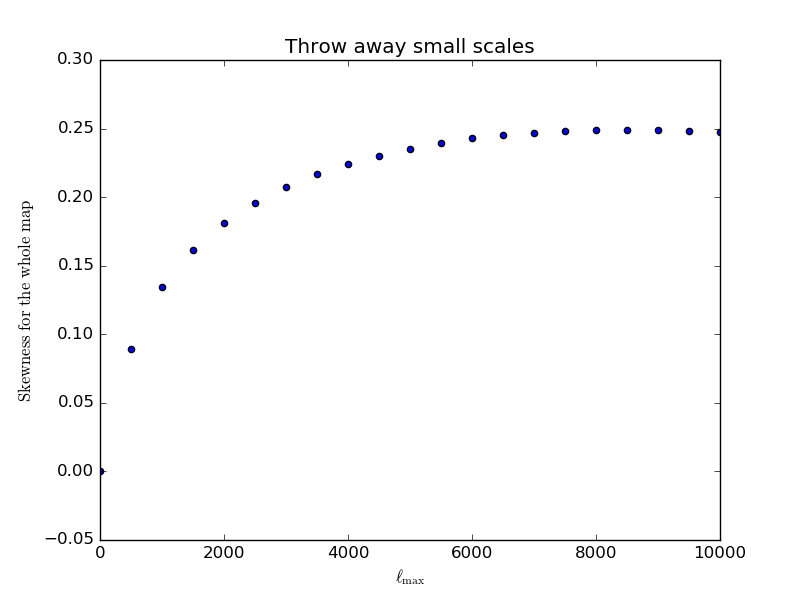
To check, we tried a top hat filter from [math]\displaystyle{ \ell }[/math] of 0 to 4000. It leads to a skewness of 0.22 and kurtosis 0.10 for the unlensed, slightly more for the lensed. Inspired by this, we look at the same exercise for the whole, unfiltered, map (again throwing away information from either the lowest or largest scales). We get
So the whole map on its own has skewness 0.25; by throwing stuff away we reduce this number.