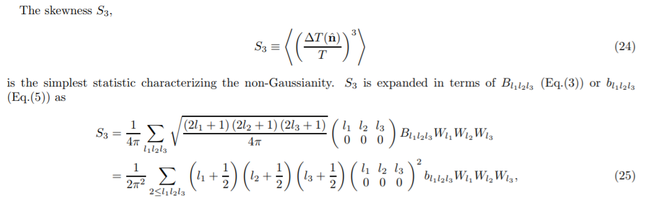June 9th, 2019 - Accuracy of the Wigner 3j Approximation

Earlier today, Alex sent us an e-mail showing that the Wigner 3j approximation we've been using (https://iopscience.iop.org/article/10.1088/0004-637X/760/1/5/pdf) is quite accurate down to an [math]\displaystyle{ \ell }[/math] of around 50 (1%).

I took it a bit further and did some more analysis.

Accuracy of [math]\displaystyle{ b_{\ell} }[/math] ([math]\displaystyle{ 0 \le \ell \lt 200 }[/math])

Since [math]\displaystyle{ b_{\ell} }[/math] is proportional to the square of the Wigner 3j symbols (left), I plotted the ratio of the exact squared and approximation squared to check the accuracy of my bispectrum estimation (right, bottom panel).

The approximation is accurate to 1% down to [math]\displaystyle{ \ell = 100 }[/math] and 2% down to [math]\displaystyle{ \ell = 50 }[/math].

While this is reassuring, one thing to note is that the ratio falls below 0.95 at around [math]\displaystyle{ \ell = 20 }[/math] (bottom panel).

Because the [math]\displaystyle{ b_{\ell} }[/math] I have been calculating is using the sum of the 200 values within each band, a large discrepancy between the exact and the approximate values for even a small number of [math]\displaystyle{ \ell }[/math]s in the first band may cause a large difference.

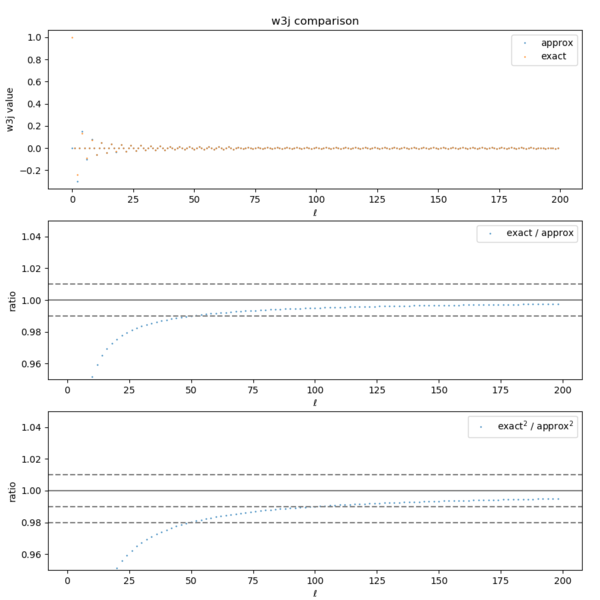
Accuracy of the 1st Band ([math]\displaystyle{ b_{\ell} }[/math])

Taking this into account, I calculated the ratios of the sums (within each band) for the first three bands.

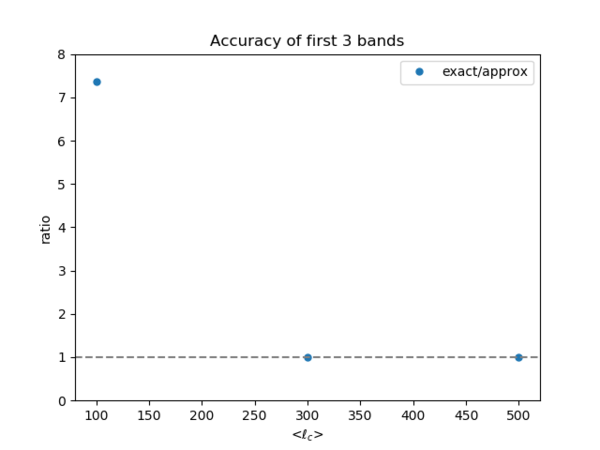
Apparently, the approximate value for the first band is 7.37 times smaller than the exact value (the exact Wigner 3j value at [math]\displaystyle{ \ell = 0 }[/math] is more than 7 times larger than the approximate value; and as seen above, the absolute values of the Wigner 3j decrease rapidly as [math]\displaystyle{ \ell }[/math] increases). Taking this into consideration, the plot comparing the Planck values to the sims values for the CIB 3 frequencies show a much better agreement for the first band. (Left: before the correction, Right: after the correction)

The errors for the next two bands are less than 1%.

Conclusion

The [math]\displaystyle{ b_{\ell} }[/math] value for the very first band can be corrected using the exact Wigner 3j value. Using this, we see a better match with Planck values. The next step is to add error bars for the Planck values; by finding the covariance matrices on the Planck Legacy Archive, and running the calculations with Planck maps (also from the Archive).