Sept 1st, 2019 - CIB non-Gaussianity: Whitening II

From LSS Mocks
Jump to navigation Jump to search 
I realized that the previous post (https://mocks.cita.utoronto.ca/index.php/Aug_26th,_2019_-_CIB_non-Gaussianity:_Whitening_of_the_Maps) needs some revisions; the CAMB maps (1) (2) were generated from the [math]\displaystyle{  D_{\ell}  }[/math] instead of the [math]\displaystyle{  C_{\ell}  }[/math], and as Professor Bond pointed out, I had been using the full CIB without the mean subtracted out for maps (4), (5), and (6). So this time, I took [math]\displaystyle{  \ln(I_{\text{map}}) - \lt  \ln(I_{\text{map}}) \gt   }[/math] for each of the maps before going through the whitening procedure (by dividing by the square root of [math]\displaystyle{  C_{\ell}  }[/math]). (For CMB maps, I added 2.73K.) Below are the results of six different maps whitened and zoomed in:

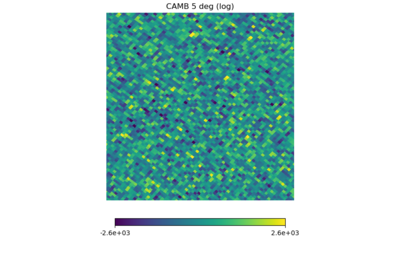
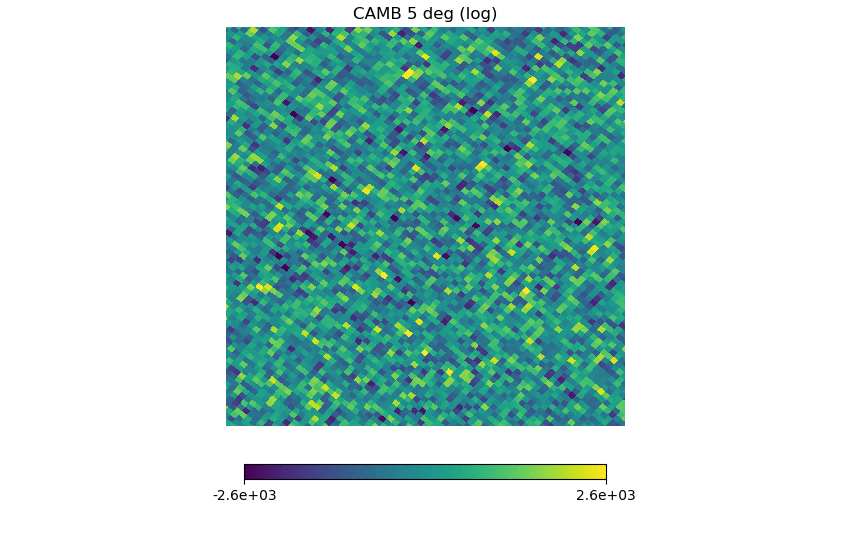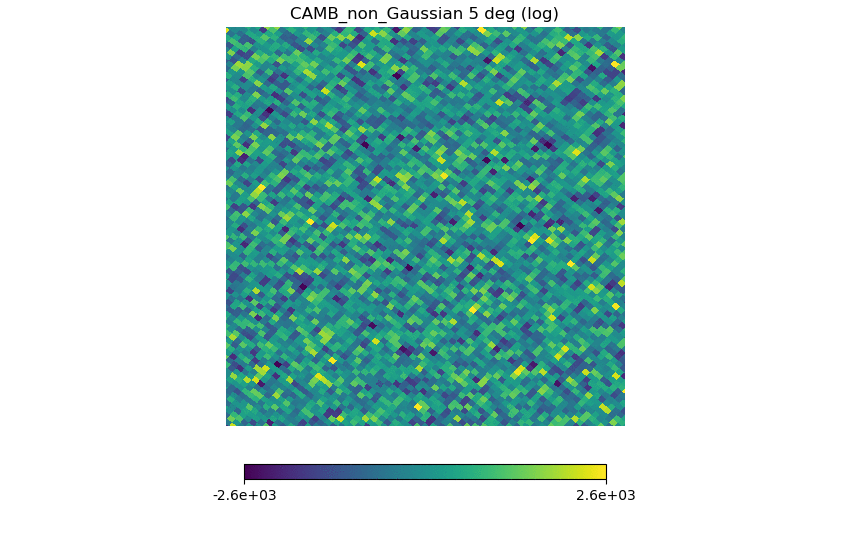
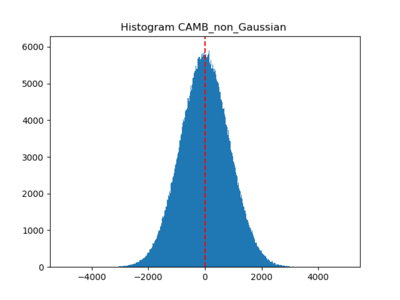
(1) an NSIDE 1024 CMB map generated from CAMB theory [math]\displaystyle{ C_{\ell} }[/math]

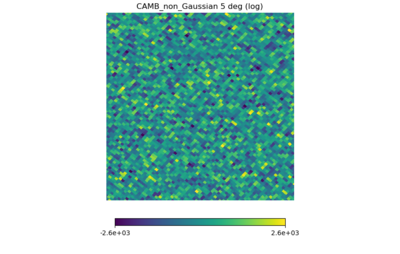
(2) a non-Gaussian map created by [math]\displaystyle{ (1) + 10 \times (1)^2 }[/math] (NSIDE = 1024)

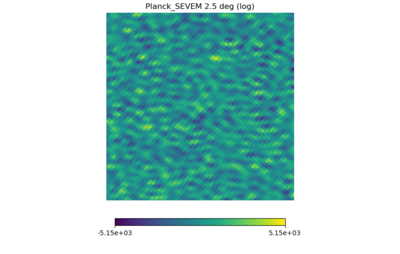
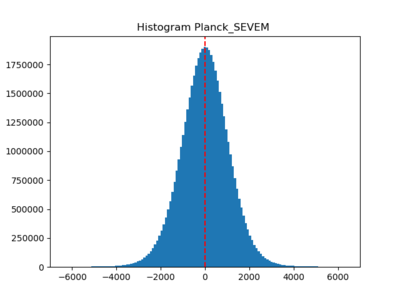
(3) the Planck SEVEM map (https://pla.esac.esa.int/#maps) (NSIDE = 2048)

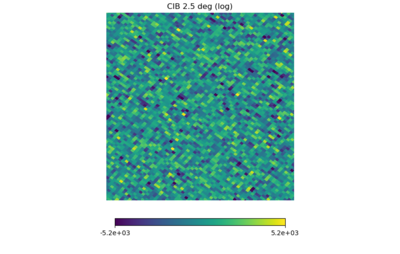
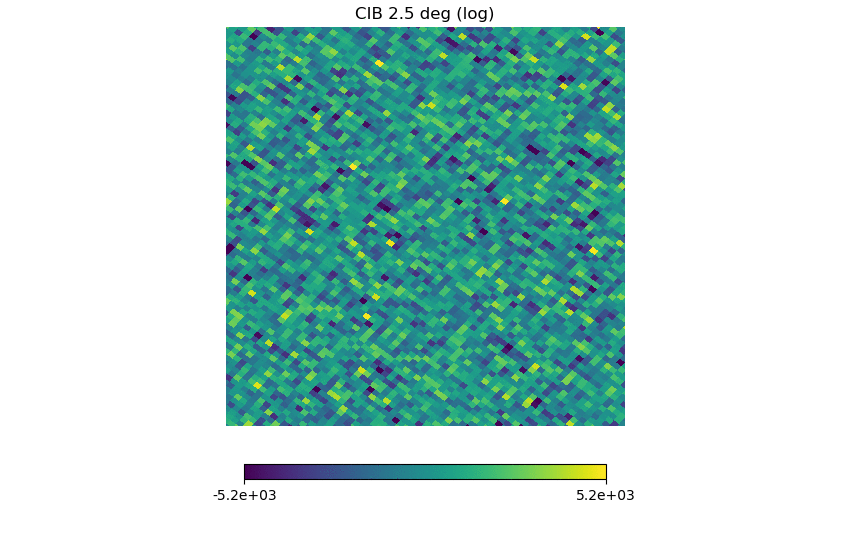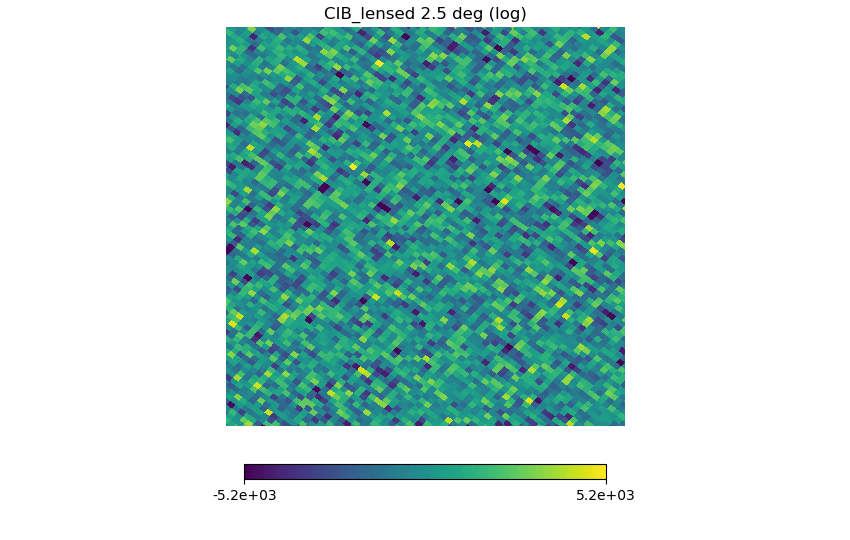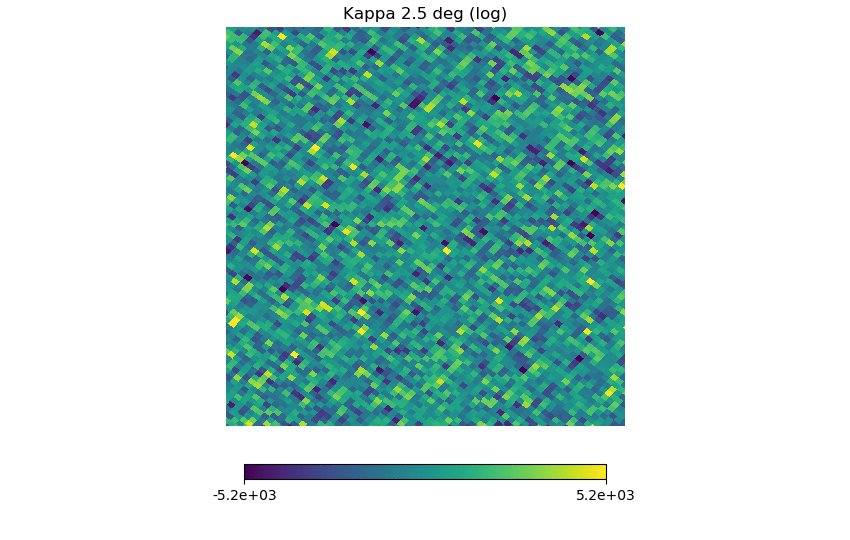
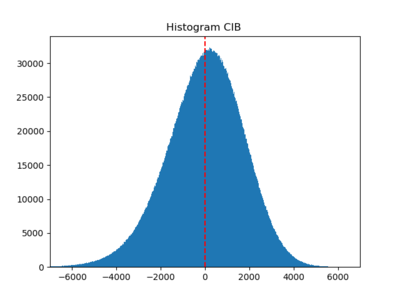
(4) the Websky CIB map (NSIDE downgraded to 2048)

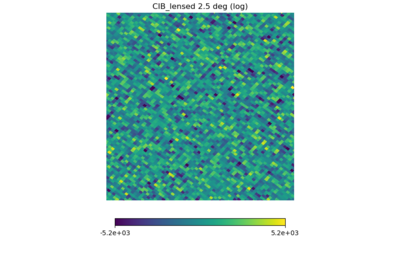
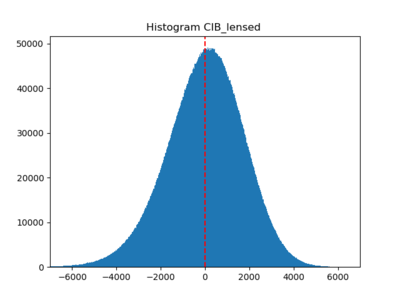
(5) the Websky CIB lensed map (NSIDE downgraded to 2048)

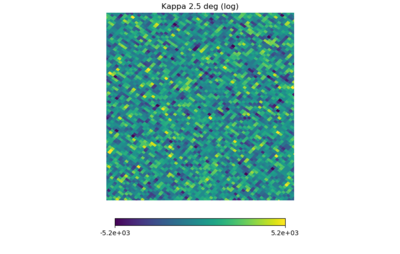
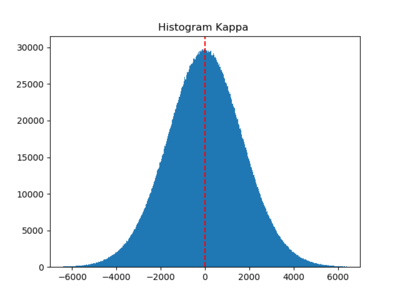
(6) the CIB halo kappa map (NSIDE downgraded to 2048)

Zoom-in maps

For each map, the range of the color bars are: [math]\displaystyle{ \mu \pm 3\sigma }[/math], with [math]\displaystyle{ \mu }[/math] being the means.

(1) (2)

Cv CAMB log.png Cv CAMB non Gaussian log.png

(3) (4)

Cv Planck SEVEM log.png Cv CIB log.png

(5) (6)

Cv CIB lensed log.png Cv Kappa log.png

Again, the first map should set the standard for a whitened Gaussian map, the second one looks different (as it must be non-Gaussian from the definition) but not as different as the previous post, the third one seems to have some kind of structure in it (but it's a Planck map), and (4), (5), (6) have similarities but seem pretty Gaussian.

Below are the CMB (and its non-Gaussian version) and CIB (CIB, CIB lensed, CIB kappa) related zoom-ins switching back and forth.

CMB

CAMB_log.gif

CIB

CIB_log.gif

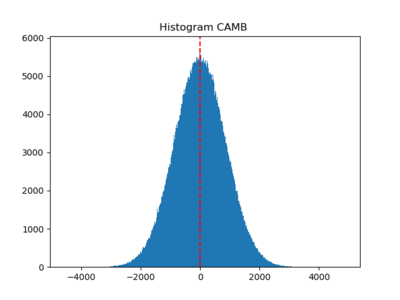
Histograms

I also checked the histograms; taking the log and subtracting out the mean before going through the whitening procedure generally make the histograms look more Gaussian ((4) (5) (6)).

(1) (2)

Hist CAMB log.png Hist CAMB non Gaussian log.png

(3) (4)

Hist Planck SEVEM log.png Hist CIB log.png

(5) (6)

Hist CIB lensed log.png Hist Kappa log.png

We see that (1) (CAMB) (2) (non-Gaussian? CAMB) (3) Planck SEVEM are close to Gaussian, and (4), (5), and (6) are weakly non-Gaussian but less so compared to the previous post.

The fact that (2) is Gaussian is bizarre; perhaps the logarithm reduces the effect of the factor of 10, but even when I multiplied by [math]\displaystyle{ 10^7 }[/math], there wasn't much difference (this could be a simple bug, which I will take a look at).

Retrieved from "https://mocks.cita.utoronto.ca/index.php?title=Sept_1st,_2019_-_CIB_non-Gaussianity:_Whitening_II&oldid=1845"