Sept 30th, 2019 - Masking vs. Removing 1st 100Mpcs

We (Alex, Pavel, and I) agreed last week that: 

1. I should mask the CIB and lensed CIB maps using the flux cut value in the Crawford paper (https://iopscience.iop.org/article/10.1088/0004-637X/784/2/143/pdf)

2. I should remove the first 100Mpcs, as the abnormally bright pixels within the first 100Mpcs contribute immensely to the bispectrum at high [math]\displaystyle{ \ell }[/math]

3. I could check whether setting the masked pixel to 0, the mean of the shell, or some other value (I used a constant value a bit larger than the flux cut value) affects the bispectrum.

Another Look at the Crawford paper's masking scheme

Near the end of section 3.3 in Crawford's paper, they state that "the 150 GHz flux cut to which this significance is equivalent varies from 5.7 mJy to 6.6 mJy. In some versions of the bispectrum analysis, we also interpolate over galaxy clusters above a given mass from the Reichardt et al. (2013) catalog."

For now, I am assuming we do not need to consider the latter part of the above excerpt, as long as our results make sense.

In a previous post, I used 6.6mJy and converted to the corresponding flux cut in a 545GHz, NSIDE 4096 full-sky map (https://mocks.cita.utoronto.ca/index.php/Aug_13th,_2019_-_CIB_Lensing:_Effect_on_the_Reduced_Bispectrum_After_Masking_Brightest_Pixels), but this time, I used the more conservative value 5.7mJy. From calculations similar to the one provided in the previous post, the appropriate flux cut value is about 7.48MJy/sr.

Masking and Removing the 0th Shell (1st 100Mpcs)

But when I removed the 0th shell and imposed the 7.48MJy/sr flux cut value, I discovered that none of the shells had any pixels larger than 7.48MJy/sr. In fact the largest flux value in all of the shells (minus the 0th shell) is around 4.xx MJy/sr and the maximum flux value for the added map (again, without the 0th shell) is around 5MJy/sr.

So with this cut, and by removing the first 100 Mpcs, it seems we do not need to mask any pixels at all.

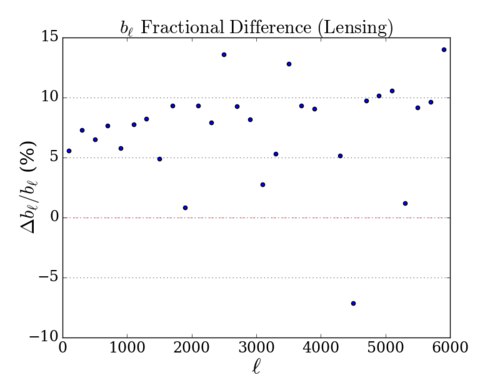
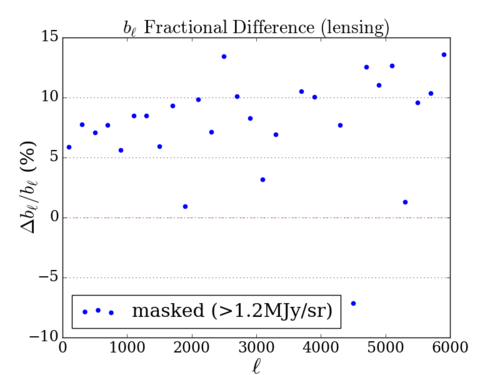
The below plots show how much lensing changes the bispectrum in comparison to a previous flux cut (including the 1st 100Mpcs but with a much stricter flux cut (1.2 MJy/sr) (this was used to match the number of pixels masked to another paper mentioned in the previous post))

Left: (Without First 100 Mpcs)  Right: (Masked ( >1.2MJy/sr))

The two look quite similar at first sight. Below is the plot of the difference between the two plots above.

While there certainly is a difference between the two plots, they are not radically different. Also, the difference between the 1st plot (without the first 100Mpcs) and the other masked (flux cut at 8.7MJy/sr or 6.6mJy, from the previous post) plot (right plot in the 1st section of https://mocks.cita.utoronto.ca/index.php/Aug_13th,_2019_-_CIB_Lensing:_Effect_on_the_Reduced_Bispectrum_After_Masking_Brightest_Pixels) is much larger, which I do not show here.

There is a little worry that the closest (100~400Mpcs) of the remaining 19 shells (corresponding to 100~7600Mpcs) still contains several bright pixels (between 2~4.xx MJy/sr), but I believe the above comparison shows that removing the first 100Mpcs sufficiently captures the change in bispectrum due to lensing especially at [math]\displaystyle{ \ell \lt 3000 }[/math].

Bispectrum Fractional Difference (Due to Lensing) by the Value of the Masked Pixel

While the analysis above shows that masking is no longer important in this project, I took a look at the difference arising from the value used for the masked pixels. The default here is the masked pixels being set to the mean of a  shell  (which is less than 0.1MJy/sr for all shells). Other variations were setting them to 0, and to 1.5MJy/sr (which I thought would be a good approximation for the Gaussian peak, but perhaps not). 

Left: Masked(mean) - Masked(0) (Fractional Difference of Lensing) Right: Masked(mean) - Masked(1.5MJy/sr) (Fractional Difference of Lensing)

As expected, setting the masked pixels to 0 do not show much difference, while setting them to 1.5MJy/sr show a noticeable difference. We see that the difference rises with higher [math]\displaystyle{ \ell }[/math].